Ing Mathematik: Funktionen

Definiton

Funktion: A und B seien Mengen. Eine Funktion f ist eine Vorschrift, die jedem Element $x\in A$ dabei genau ein Element $f(x)\in B$ zuordnet (eindeutige Abbildung).

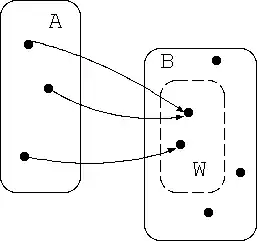
A heißt Definitionsbereich von f, B ist der Zielbereich und W der Wertebereich von f. $x\in A$ nennt man Argument von f. $y\in B$ mit $y=\ f(x)$ bezeichnet man als "Bild von x unter f" oder "Funktionswert von f an der Stelle x".

Eine Funktion kann auch in Form eines Pfeildiagramms visualisiert werden

Verschiedene Schreibweisen

Exakte Darstellung: $f:\ \left\{(x,y)\ |\ y=f(x),\ x\in A,\ y\in B\right\}$
Abgekürzte Schreibweisen:
- Funktion f von A nach B: $f:\ A\rightarrow B$
- $f:\ x\mapsto f(x)$
- $x\mapsto f(x)$
- Funktionsgleichung in expliziter Form: $y=\ f(x)$
- Funktionsgleichung in impliziter Form: $F(x,y)=\ 0$
- Funktionsgleichung in Parameterform: ${\begin{matrix}x=\varphi (t)\\y=\psi (t)\end{matrix}}$

Zwei Funktionen f und g sind dann gleich, wenn folgender Zusammenhang gilt:

$f=g\;\Leftrightarrow \;\forall x\in A\ :\ f(x)=g(x)$

Komposition von Funktionen

Beispiel: Die Schallgeschwindigkeit c ist bei gleichbleibendem Druck und Dichte des Mediums abhängig vom Isentropenkoeffizienten $\kappa \$ . Das bedeutet $c=\ f(\kappa )$ . Gleichzeitig ist aber $\kappa \$ abhängig von der Temperatur T, also $\kappa =\ g(T)$ .

Die Zusammensetzung (Komposition) ergibt $c=h(T)=f\left(g(T)\right)$

Man schreibt für $f\left(g(x)\right)$ auch $(f\circ g)(x)$ . Es ist auch zu beachten, dass $f\circ g\neq g\circ f$

Formal kann eine Komposition von Funktionen folgendermaßen angeschrieben werden:

$g:\ A\rightarrow B,\quad f:\ C\rightarrow D,\quad B=C$

$f\circ g:\ A\rightarrow D$ .

Bijektivität und Umkehrung

Injektive Funktionen

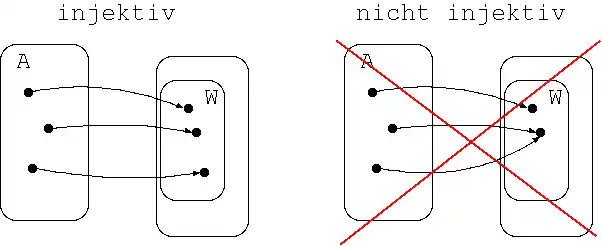
Injektive Funktion: Eine Funktion $f:\ A\rightarrow B$ heißt injektiv (eineindeutig), wenn $f\left(x_{1}\right)=f\left(x_{2}\right)\;\Rightarrow \;x_{1}=x_{2}$

Ist eine Funktion f injektiv und $a\in W$ , so läßt sich eine Gleichung $f(x)=\ a$ prinzipiell eindeutig nach x auflösen.

Beispiel: $x^{2}=\ a$ ist nicht injektiv, da $x=\pm {\sqrt {a}}$

Surjektive Funktionen

Gilt, dass der Wertebereich W einer Funktion f gleich dem Zielbereich B ist, so nennt man die Funktion surjektiv. Eine surjektive Funktion muss nicht unbedingt injektiv sein.

Bijektive Funktionen

Ist eine Funktion f sowohl injektiv als auch surjektiv, so nennt man sie bijektiv. Zu jeder bijektiven Funktion $f:\ A\rightarrow B$ existiert die Umkehrfunktion $f^{-1}:\ B\rightarrow A$ .

Umkehrfunktionen

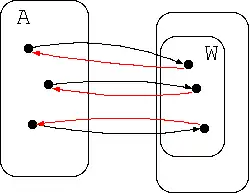
Umkehrfunktion: Ist $f:\ A\rightarrow W$ eine injektive Funktion, so ist $f^{-1}:\ W\rightarrow A$ die Umkehrfunktion zu f. $f^{-1}(y)=x\;\leftrightarrow \;y=f(x);\;x\in A$ .

Monotonie und Beschränktheit

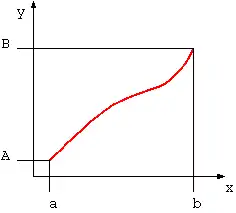
Monotone Funktionen: Eine Funktion y=f(x) ist genau dann monoton steigend (fallend), wenn $\textstyle f(x)\geq f(y)$ , bzw. $\textstyle f(x)\leq f(y)$ für alle $\textstyle x>y$ ist.; Eine weitere Unterscheidung ist "streng monoton steigend/fallend", wenn $\textstyle f(x)>f(y)$ , bzw. $\textstyle f(x)<f(y)$ für alle $\textstyle x>y$ gilt.

Monoton steigende Funktion: Wird x größer, so wird auch y=f(x) größer oder bleibt zumindest gleich.

Beispiel:

Monoton fallende Funktion: Wird x größer, so wird y=f(x) kleiner oder bleibt zumindest gleich.

Beispiel:

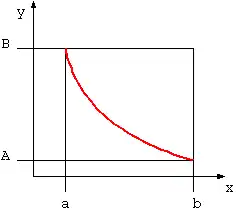
Beschränkte Funktionen: Eine Funktion heißt beschränkt, wenn es zwei Zahlen $S_{1}$ und $S_{2}$ gibt, sodass $S_{1}\leq f(x)\leq S_{2}$ für alle x gilt.

Beispiel: $\sin(x)$ und $\cos(x)$ sind beschränkte Funktionen mit $S_{1}=-1$ und $S_{2}=1$ .

Bezug zur Monotonie

Satz Jede streng monotone Funktion ist injektiv. Die Umkehrung gilt im Allgemeinen nicht (kann aber).

Weitere Eigenschaften

Symmetrische (gerade) Funktion: Ein Funktion heißt symmetrisch (zur Ordinate), wenn gilt f(x) = f(-x)

Beispiele: $y=\cos(x)$ , $y=x^{2}$

Schiefsymmetrische (ungerade) Funktion: Ein Funktion heißt schiefsymmetrisch, wenn gilt f(-x) = -f(x)
Dies entspricht einer Spiegelung der Funktion an der Winkelhalbierenden

Beispiele: $y=\sin(x)$ , $y=x^{3}$

Periodische Funktion: $f(x)=f(x\pm kT)$ , wobei T als Periode der Funktion bezeichnet wird.

Beispiel: f(x)=sin(x) Periode T=Pi/2

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.