Formelsammlung Statistik/ Deskriptive Statistik

Skalenniveaus

Nominalskala

Die Ausprägungen des nominalskalierten Merkmals können nicht geordnet werden,

man kann sie nur vergleichen und abzählen.

Es handelt sich um qualitative Merkmale. Erhalten die Ausprägungen Ziffern zugeordnet,

handelt es sich nur um eine Verschlüsselung (Codierung): 1 = männlich, 2 = weiblich.

Ordinalskala

Zwischen den Ausprägungen des ordinalskalierten (rangskalierten) Merkmals existiert eine Beziehung

der Form mehr oder weniger, < oder >, besser oder schlechter.

Eine Quotientenbildung macht wenig Sinn (Beispiel Noten: 1, 2, 3, 4, 5).

Intervallskala

Die Abstände zwischen den Ausprägungen des (quantitativen) Merkmals der Intervallskala

können gemessen werden. Es handelt sich bei den Ausprägungen um (reelle) Zahlen.

Beispiel: Kinderzahl, Temperatur.

Verhältnissskala

Sowohl die Abstände als auch Verhältnisse zwischen den Ausprägungen des (quantitativen) Merkmals

können gemessen werden. Es handelt sich bei den Ausprägungen um (reelle) Zahlen. Beispiel: Einkommen.

Zweig-Blätter-(stem-leaf-) Diagramm

Die linke Spalte enthält als „Stämme“ die Äquivalenzklassen, in die die auf der rechten Seite als „Blätter“

dargestellten Merkmale eingeteilt werden. Beispiel: Gegeben sind die Werte 0,3 0,4 2,5 2,5 2,6 2,7 2,8 3,5 3,7.

Wählt man die natürlichen Zahlen als Klasseneinteilung, ergibt sich folgendes Stamm-Blatt-Diagramm:

3	5	7
2	5	5	6	7	8
1
0	3	4

Lageparameter

Arithmetisches Mittel

{\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}

Median (Zentralwert)

Sind die Beobachtungswerte der Größe nach geordnet, ist der Median z die Stelle, die die Teilgesamtheit in zwei gleiche Hälften teilt.

z={\begin{cases}x_{[{\frac {n+1}{2}}]}&{\text{n ungerade }}\\{\frac {1}{2}}(x_{[{\frac {n}{2}}]}+x_{[{\frac {n}{2}}+1]})&{\text{n gerade}}\\\end{cases}}

geometrisches Mittel

{\bar {X}}_{geom}={\sqrt[{n}]{\prod _{i=1}^{n}x_{i}}}

harmonisches Mittel

{\bar {X}}_{harm}={\frac {n}{\sum \limits _{i=1}^{n}{\frac {^{1}}{x_{i}}}}}

Modalwert

Der am häufigsten auftretende Wert

Varianz

Grundgesamtheit:

\sigma ^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}

Stichprobe:

{\bar {s}}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {X}})^{2}

Verschiebungssatz

Für jedes $c\in \mathbb {R}$ gilt

\sum _{i=1}^{n}(x_{i}-c)^{2}=\sum _{i=1}^{n}(x_{i}-{\bar {X}})^{2}+n({\bar {X}}-c)^{2}

Damit erhält man als Varianz

s^{2}={\frac {1}{n}}(\sum _{i=1}^{n}x_{i}^{2}-n\cdot {\bar {X}}^{2})

Variationskoeffizient

v={\frac {\bar {s}}{\bar {X}}},\;\;{\bar {X}}>0

Konzentrationsmasse

Konzentrationsrate

Die Konzentrationsrate CRn ist die Summe der Marktanteile der n größten Unternehmen eines relevanten Marktes. Im GWB werden die Raten CR₁, CR₃ und CR₅ herangezogen.

Lorenzkurve

Für eine geordnete Urliste x₁ ≤ x₂… ≤x_n trägt man die kumulierte relative Merkmalssumme

$q_{i}={\frac {\sum \limits _{k=1}^{j}x_{i}}{\sum \limits _{k=1}^{n}x_{i}}}$

über den Anteil der Merkmalsträger $p_{j}={\frac {j}{n}}$ auf.

Liegen die Merkmale in gruppierter Form vor, trägt man die kumulierte relative Merkmalssumme

$q_{i}={\frac {\sum \limits _{k=1}^{j}x_{i}}{\sum \limits _{k=1}^{n}x_{i}}}$

über der Häufigkeit $p_{i}={\frac {1}{n}}\cdot \sum _{j=1}^{i}h_{j}$ auf.

Zwischen (0;0) und (1;1) wird die Winkelhalbierende des Koordinatensystems eingetragen.

Gini-Koeffizient

Als Ginikoeffizient G bezeichnet man das Verhältnis der Fläche zwischen Winkelhalbierender und der Lorenzkurve

zur Gesamtfläche unter der Winkelhalbierenden (= 1/2).

Die Fläche unterhalb der Lorenzkurve kann man einfach aus Teil-Trapezflächen zusammensetzen:

G=\left({\frac {1}{2}}-{\frac {1}{2}}\sum _{i=1}^{n}\Delta p_{i}\cdot (q_{i-1}+q_{i})\right):{\frac {1}{2}}=1-\sum _{i=1}^{n}(p_{i}-p_{i-1})\cdot (q_{i-1}+q_{i})

(p₀ = 0 ; q₀ = 0):

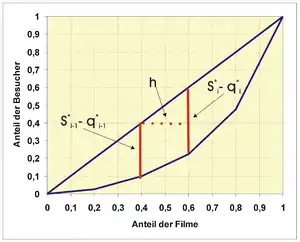Ginikoeffizient: Ermittlung einer Trapezfläche für i=3
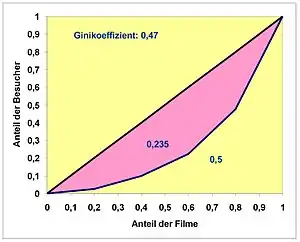Ginikoeffizient

Herfindahl-Index

H=\sum \limits _{i=1}^{n}p_{i}^{2},{\mbox{wobei }}p_{i}={\frac {x_{i}}{\sum \limits _{j=1}^{n}x_{j}}}

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.