Graphen

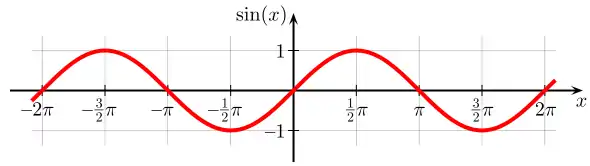
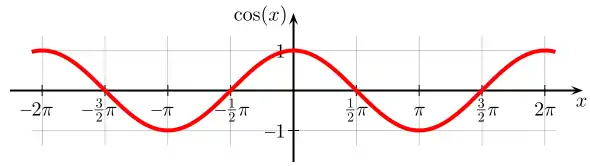
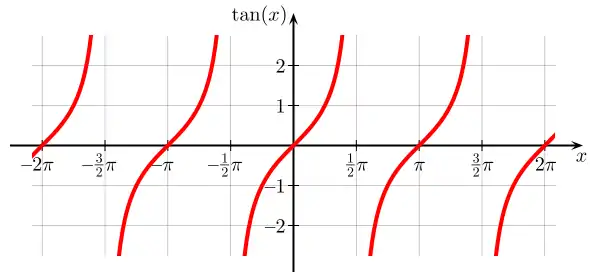
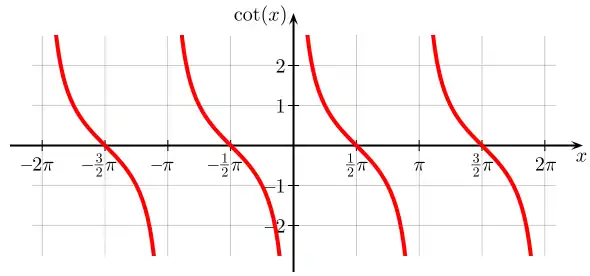
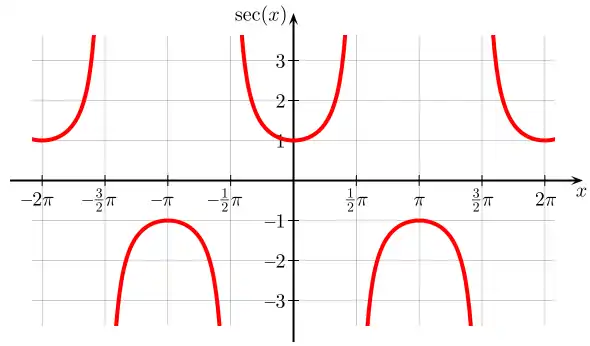
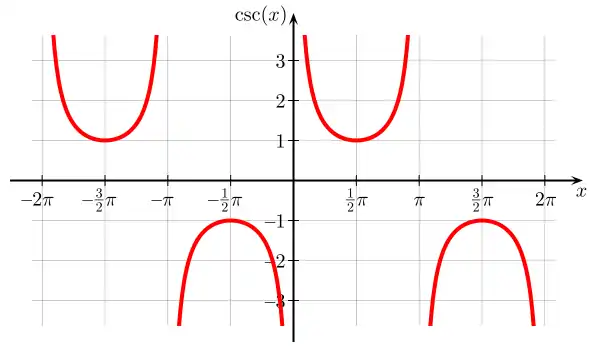
Symmetrien

Definition der Winkel- und Hyperbelfunktionen durch die e-Funktion

${\displaystyle \sin(z)={\frac {\mathrm {e} ^{\mathrm {i} z}-\mathrm {e} ^{-\mathrm {i} z}}{2\mathrm {i} }}}$	${\displaystyle \sinh(z)={\frac {\mathrm {e} ^{z}-\mathrm {e} ^{-z}}{2}}}$	${\displaystyle \sin(\mathrm {i} z)=\mathrm {i} \sinh(z)\,}$	${\displaystyle \sinh(\mathrm {i} z)=\mathrm {i} \sin(z)\,}$
${\displaystyle \cos(z)={\frac {\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}}{2}}}$	${\displaystyle \cosh(z)={\frac {\mathrm {e} ^{z}+\mathrm {e} ^{-z}}{2}}}$	${\displaystyle \cos(\mathrm {i} z)=\cosh(z)\,}$	${\displaystyle \cosh(\mathrm {i} z)=\cos(z)\,}$
${\displaystyle \tan(z)={\frac {1}{\mathrm {i} }}\,{\frac {\mathrm {e} ^{\mathrm {i} z}-\mathrm {e} ^{-\mathrm {i} z}}{\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}}}}$	${\displaystyle \tanh(z)={\frac {\mathrm {e} ^{z}-\mathrm {e} ^{-z}}{\mathrm {e} ^{z}+\mathrm {e} ^{-z}}}}$	${\displaystyle \tan(\mathrm {i} z)=\mathrm {i} \tanh(z)\,}$	${\displaystyle \tanh(\mathrm {i} z)=\mathrm {i} \tan(z)\,}$
${\displaystyle \cot(z)=\mathrm {i} \,{\frac {\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}}{\mathrm {e} ^{\mathrm {i} z}-\mathrm {e} ^{-\mathrm {i} z}}}}$	${\displaystyle \coth(z)={\frac {\mathrm {e} ^{z}+\mathrm {e} ^{-z}}{\mathrm {e} ^{z}-\mathrm {e} ^{-z}}}}$	${\displaystyle \cot(\mathrm {i} z)={\frac {1}{\mathrm {i} }}\coth(z)\,}$	${\displaystyle \coth(\mathrm {i} z)={\frac {1}{\mathrm {i} }}\cot(z)\,}$
${\displaystyle \sec(z)={\frac {2}{\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}}}}$	${\displaystyle \operatorname {sech} (z)={\frac {2}{\mathrm {e} ^{z}+\mathrm {e} ^{-z}}}}$	${\displaystyle \sec(\mathrm {i} z)=\operatorname {sech} (z)}$	${\displaystyle \operatorname {sech} (\mathrm {i} z)=\sec(z)}$
${\displaystyle \csc(z)={\frac {2\mathrm {i} }{\mathrm {e} ^{\mathrm {i} z}-\mathrm {e} ^{-\mathrm {i} z}}}}$	${\displaystyle \operatorname {csch} (z)={\frac {2}{\mathrm {e} ^{z}-\mathrm {e} ^{-z}}}}$	${\displaystyle \csc(\mathrm {i} z)={\frac {1}{\mathrm {i} }}\,\operatorname {csch} (z)}$	${\displaystyle \operatorname {csch} (\mathrm {i} z)={\frac {1}{\mathrm {i} }}\,\csc(z)}$

Gegenseitige Darstellbarkeit von Winkelfunktionen

	sin	cos	tan	cot	sec	csc
sin2(x)	${\displaystyle \sin ^{2}(x)}$	${\displaystyle 1-\cos ^{2}(x)}$	${\displaystyle {\frac {\tan ^{2}(x)}{1+\tan ^{2}(x)}}}$	${\displaystyle {\frac {1}{\cot ^{2}(x)+1}}}$	${\displaystyle {\frac {\sec ^{2}(x)-1}{\sec ^{2}(x)}}}$	${\displaystyle {\frac {1}{\csc ^{2}(x)}}}$
cos2(x)	${\displaystyle 1-\sin ^{2}(x)}$	${\displaystyle \cos ^{2}(x)}$	${\displaystyle {\frac {1}{1+\tan ^{2}(x)}}}$	${\displaystyle {\frac {\cot ^{2}(x)}{\cot ^{2}(x)+1}}}$	${\displaystyle {\frac {1}{\sec ^{2}(x)}}}$	${\displaystyle {\frac {\csc ^{2}(x)-1}{\csc ^{2}(x)}}}$
tan2(x)	${\displaystyle {\frac {\sin ^{2}(x)}{1-\sin ^{2}(x)}}}$	${\displaystyle {\frac {1-\cos ^{2}(x)}{\cos ^{2}(x)}}}$	${\displaystyle \tan ^{2}(x)}$	${\displaystyle {\frac {1}{\cot ^{2}(x)}}}$	${\displaystyle \sec ^{2}(x)-1}$	${\displaystyle {\frac {1}{\csc ^{2}(x)-1}}}$
cot2(x)	${\displaystyle {\frac {1-\sin ^{2}(x)}{\sin ^{2}(x)}}}$	${\displaystyle {\frac {\cos ^{2}(x)}{1-\cos ^{2}(x)}}}$	${\displaystyle {\frac {1}{\tan ^{2}(x)}}}$	${\displaystyle \cot ^{2}(x)}$	${\displaystyle {\frac {1}{\sec ^{2}(x)-1}}}$	${\displaystyle \csc ^{2}(x)-1}$
sec2(x)	${\displaystyle {\frac {1}{1-\sin ^{2}(x)}}}$	${\displaystyle {\frac {1}{\cos ^{2}(x)}}}$	${\displaystyle 1+\tan ^{2}(x)}$	${\displaystyle {\frac {\cot ^{2}(x)+1}{\cot ^{2}(x)}}}$	${\displaystyle \sec ^{2}(x)}$	${\displaystyle {\frac {\csc ^{2}(x)}{\csc ^{2}(x)-1}}}$
csc2(x)	${\displaystyle {\frac {1}{\sin ^{2}(x)}}}$	${\displaystyle {\frac {1}{1-\cos ^{2}(x)}}}$	${\displaystyle {\frac {1+\tan ^{2}(x)}{\tan ^{2}(x)}}}$	${\displaystyle \cot ^{2}(x)+1}$	${\displaystyle {\frac {\sec ^{2}(x)}{\sec ^{2}(x)-1}}}$	${\displaystyle \csc ^{2}(x)}$

Die Gleichungen gelten für alle ${\displaystyle x\in \mathbb {R} }$ mit Ausnahme der Polstellen. Stetig hebbare Definitionslücken können entsprechend ergänzt werden.

Man beachte, dass die Gleichungen nach dem Wurzelziehen nur betragsmäßig gültig sind, da beim Quadrieren die Vorzeichen verloren gehen.

Winkelfunktionen mit verschobenem Argument

	${\displaystyle \pm \varphi }$	${\displaystyle {\frac {\pi }{2}}\pm \varphi }$	${\displaystyle \pi \pm \varphi }$	${\displaystyle {\frac {3\pi }{2}}\pm \varphi }$
${\displaystyle \sin \,}$	${\displaystyle \pm \sin }$	${\displaystyle \cos \!}$	${\displaystyle \mp \sin }$	${\displaystyle -\cos \!}$
${\displaystyle \cos \,}$	${\displaystyle \cos \!}$	${\displaystyle \mp \sin \!}$	${\displaystyle -\cos \!}$	${\displaystyle \pm \sin \!}$
${\displaystyle \tan \,}$	${\displaystyle \pm \tan \!}$	${\displaystyle \mp \cot \!}$	${\displaystyle \pm \tan \!}$	${\displaystyle \mp \cot \!}$
${\displaystyle \cot \,}$	${\displaystyle \pm \cot \!}$	${\displaystyle \mp \tan \!}$	${\displaystyle \pm \cot \!}$	${\displaystyle \mp \tan \!}$
${\displaystyle \sec \,}$	${\displaystyle \sec \!}$	${\displaystyle \mp \csc \!}$	${\displaystyle -\sec \!}$	${\displaystyle \pm \csc \!}$
${\displaystyle \csc \,}$	${\displaystyle \pm \csc }$	${\displaystyle \sec \!}$	${\displaystyle \mp \csc }$	${\displaystyle -\sec \!}$

${\displaystyle 1+\tan \left({\frac {\pi }{4}}-x\right)={\frac {2}{1+\tan x}}}$

Additionstheoreme

${\displaystyle \sin(x\pm y)=\sin x\;\cos y\pm \sin y\;\cos x}$

${\displaystyle \cos(x\pm y)=\cos x\;\cos y\mp \sin x\;\sin y}$

${\displaystyle \tan(x\pm y)={\frac {\tan x\pm \tan y}{1\mp \tan x\;\tan y}}}$

${\displaystyle \cot \left(x\pm y\right)={\frac {\pm \cot x\cot y\mp 1}{\cot x\pm \cot y}}}$

${\displaystyle \sin(x+y)\,\sin(x-y)=\cos ^{2}y-\cos ^{2}x}$

${\displaystyle \cos(x+y)\,\cos(x-y)=\cos ^{2}y-\sin ^{2}x}$

Doppelwinkelfunktionen

${\displaystyle \sin(2x)=2\,\sin x\,\cos x={\frac {2\tan x}{1+\tan ^{2}x}}}$

${\displaystyle \cos(2x)=\cos ^{2}x-\sin ^{2}x=1-2\sin ^{2}x=2\cos ^{2}x-1={\frac {1-\tan ^{2}x}{1+\tan ^{2}x}}}$

${\displaystyle \tan(2x)={\frac {2\tan x}{1-\tan ^{2}x}}={\frac {2}{\cot x-\tan x}}}$

${\displaystyle \cot(2x)={\frac {\cot ^{2}x-1}{2\cot x}}={\frac {\cot x-\tan x}{2}}}$

Winkelfunktionen für weitere Vielfache

${\displaystyle \sin(3x)=3\sin x-4\sin ^{3}x\!}$

${\displaystyle \sin(4x)=8\sin x\;\cos ^{3}x-4\sin x\;\cos x}$

${\displaystyle \sin(5x)=16\sin x\;\cos ^{4}x-12\sin x\;\cos ^{2}x+\sin x}$

${\displaystyle \sin(nx)=n\;\sin x\;\cos ^{n-1}x-{n \choose 3}\sin ^{3}x\;\cos ^{n-3}x+{n \choose 5}\sin ^{5}x\;\cos ^{n-5}x\;-\;+\;\dots }$

${\displaystyle \cos(3x)=4\cos ^{3}x-3\cos x\!}$

${\displaystyle \cos(4x)=8\cos ^{4}x-8\cos ^{2}x+1\!}$

${\displaystyle \cos(5x)=16\cos ^{5}x-20\cos ^{3}x+5\cos x\!}$

${\displaystyle \cos(nx)=\cos ^{n}x-{n \choose 2}\sin ^{2}x\;\cos ^{n-2}x+{n \choose 4}\sin ^{4}x\;\cos ^{n-4}x\;-\;+\;\dots }$

${\displaystyle \tan(nx)={\frac {\sum _{k=0}^{\infty }(-1)^{k}\,{n \choose 2k+1}\,\tan ^{2k+1}}{\sum _{k=0}^{\infty }(-1)^{k}\,{n \choose 2k}\,\tan ^{2k}}}}$

${\displaystyle \cot(nx)=(-1)^{n-1}\,\left({\frac {\sum _{k=0}^{\infty }(-1)^{k}\,{n \choose 2k+1}\,\cot ^{2k+1}}{\sum _{k=0}^{\infty }(-1)^{k}\,{n \choose 2k}\,\cot ^{2k}}}\right)^{(-1)^{n-1}}}$

Rekursionsformeln mit ${\displaystyle n,x\in \mathbb {C} }$:

${\displaystyle {\begin{aligned}\cos(nx)&=2\cos(x)\cos((n-1)x)+\cos((n-2)x),\\\sin(nx)&=2\cos(x)\sin((n-1)x)+\sin((n-2)x).\end{aligned}}}$

Halbwinkelformeln

${\displaystyle \sin {\frac {x}{2}}={\sqrt {\frac {1-\cos x}{2}}}}$ für ${\displaystyle x\in [0,2\pi ]}$

${\displaystyle \cos {\frac {x}{2}}={\sqrt {\frac {1+\cos x}{2}}}}$ für ${\displaystyle x\in [-\pi ,\pi ]}$

${\displaystyle \tan {\frac {x}{2}}={\sqrt {\frac {1-\cos x}{1+\cos x}}}={\frac {1-\cos x}{\sin(x)}}={\frac {\sin x}{1+\cos x}}}$ für ${\displaystyle x\in ]-\pi ,\pi [}$

${\displaystyle \cot {\frac {x}{2}}={\sqrt {\frac {1+\cos x}{1-\cos x}}}={\frac {1+\cos x}{\sin x}}={\frac {\sin x}{1-\cos x}}}$ für ${\displaystyle x\in ]-\pi ,\pi [}$

Identitäten

Aus den Additionstheoremen lassen sich Identitäten ableiten:

${\displaystyle \sin x\pm \sin y=2\sin {\frac {x\pm y}{2}}\,\cos {\frac {x\mp y}{2}}}$

${\displaystyle \cos x\pm \cos y=\pm 2\;{\begin{matrix}\cos \\\sin \end{matrix}}\left({\frac {x+y}{2}}\right){\begin{matrix}\cos \\\sin \end{matrix}}\left({\frac {x-y}{2}}\right)}$

${\displaystyle \tan x\pm \tan y={\frac {\sin(x\pm y)}{\cos(x)\,\cos(y)}}\quad ,\quad \cot x\pm \cot y={\frac {\sin(y\pm x)}{\sin(x)\,\sin(y)}}}$

Produkte der Winkelfunktionen

${\displaystyle \cos x\;\cos y={\frac {\cos(x-y)+\cos(x+y)}{2}}}$

${\displaystyle \sin x\;\sin y={\frac {\cos(x-y)-\cos(x+y)}{2}}}$

${\displaystyle \sin x\;\cos y={\frac {\sin(x-y)+\sin(x+y)}{2}}}$

${\displaystyle \tan x\;\tan y={\frac {\tan x+\tan y}{\cot x+\cot y}}=-{\frac {\tan x-\tan y}{\cot x-\cot y}}}$

${\displaystyle \cot x\;\cot y={\frac {\cot x+\cot y}{\tan x+\tan y}}=-{\frac {\cot x-\cot y}{\tan x-\tan y}}}$

${\displaystyle \tan x\;\cot y={\frac {\tan x+\cot y}{\cot x+\tan y}}=-{\frac {\tan x-\cot y}{\cot x-\tan y}}}$

${\displaystyle \sin x\;\sin y\;\sin z={\frac {1}{4}}\left[\sin(x+y-z)+\sin(y+z-x)+\sin(z+x-y)-\sin(x+y+z)\right]}$

${\displaystyle \cos x\;\cos y\;\cos z={\frac {1}{4}}\left[\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)+\cos(x+y+z)\right]}$

${\displaystyle \sin x\;\sin y\;\cos z={\frac {1}{4}}\left[-\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)-\cos(x+y+z)\right]}$

${\displaystyle \sin x\;\cos y\;\cos z={\frac {1}{4}}\left[\sin(x+y-z)-\sin(y+z-x)+\sin(z+x-y)+\sin(x+y+z)\right]}$

Potenzen der Winkelfunktionen

${\displaystyle (2\cos x)^{2n}=\sum _{k=-n}^{n}{2n \choose n-k}\cos 2kx}$

${\displaystyle (2\sin x)^{2n}=\sum _{k=-n}^{n}(-1)^{k}\,{2n \choose n-k}\cos 2kx}$

${\displaystyle (2\cos x)^{2n+1}=2\sum _{k=0}^{n}{2n+1 \choose n-k}\cos(2k+1)x}$

${\displaystyle (2\sin x)^{2n+1}=2\sum _{k=0}^{n}(-1)^{k}\,{2n+1 \choose n-k}\sin(2k+1)x}$