Zurück zu Identitäten
- Ist , so gilt für .
Berechne von die Mellin-Transformierte:
Für ist
, wobei sich auf ganz meromorph fortsetzen lässt.
Für ein ist dann .
Die Funktion hat ihre Polstellen bei . Hierbei ist
.
Unter Verwendung der Legendreschen Verdopplungsformel lässt sich auch schreiben als
.
Nach der Riemannschen Funktionalgleichung ist dabei
. Also ist .
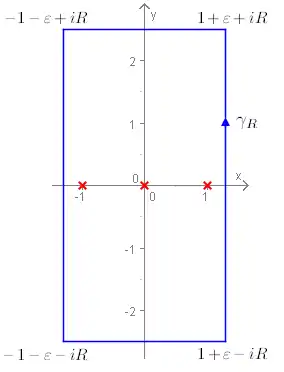
Beim Integral verschwinden die Anteile über den vertikalen Strecken für .
Nach dem Residuensatz ist nun
.
Das erste Integral ist und das zweite ist nach Substitution gleich .
- Ist , so gilt für .
Berechne von die Mellin-Transformierte:
Für ist
, wobei sich auf ganz meromorph fortsetzen lässt.
Für ein ist dann .
Die Funktion hat ihre Polstellen bei . Hierbei ist
.
Unter Verwendung der Legendreschen Verdopplungsformel lässt sich auch schreiben als
.
Nach der Riemannschen Funktionalgleichung ist dabei
. Also ist .

Beim Integral verschwinden die Anteile über den vertikalen Strecken für .
Nach dem Residuensatz ist nun
.
Das erste Integral ist und das zweite ist nach Substitution gleich .
Betrachte die Formel
.
Multipliziere mit durch und differenziere nach :
Substituiere und :
Die Funktion besitzt also die Kosinus-Fouriertransformierte
.
Nach der Poissonschen Summationsformel ist
.
In dieser Gleichung lässt sich durch ersetzen.
Begründung: Für ist .
Setzt man , so ist .