Definition

Eigenschaften

Wenn ${\displaystyle m,n}$ teilerfremd sind, d. h. wenn ${\displaystyle \operatorname {ggT} (m,n)=1}$ ist, so gilt:

${\displaystyle \varphi (mn)=\varphi (m)\,\varphi (n).}$

Ist ${\displaystyle p^{k}}$ eine Primzahlpotenz mit ${\displaystyle k\in \mathbb {Z} }$ und ${\displaystyle k\geq 1}$, so gilt:

${\displaystyle \varphi (p^{k})={\Big (}1-{\frac {1}{p}}{\Big )}p^{k}=(p-1)p^{k-1}=p^{k}-p^{k-1}.}$

Für die Primfaktorzerlegung

${\displaystyle n=\prod _{p|n}p^{k_{p}}}$

gilt:

${\displaystyle \varphi (n)=\prod _{p|n}(p^{k_{p}}-p^{{k_{p}}-1})=n\prod _{p|n}{\Big (}1-{\frac {1}{p}}{\Big )}.}$

Meint man mit ${\displaystyle d|n}$, dass die ${\displaystyle d}$ aus der Teilermenge von ${\displaystyle n}$ entstammen, so gilt:

${\displaystyle n=\sum _{d|n}\varphi (d).}$

Möbius-Inversion der letzten Formel:

${\displaystyle \varphi (n)=\sum _{d|n}d\cdot \mu {\Big (}{\frac {n}{d}}{\Big )}=n\sum _{d|n}{\frac {\mu (d)}{d}}.}$

Wertetabelle

${\displaystyle \varphi (n)}$	+0	+1	+2	+3	+4	+5	+6	+7	+8	+9
00+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60
100+	40	100	32	102	48	48	52	106	36	108
110+	40	72	48	112	36	88	56	72	58	96
120+	32	110	60	80	60	100	36	126	64	84
130+	48	130	40	108	66	72	64	136	44	138
140+	48	92	70	120	48	112	72	84	72	148
150+	40	150	72	96	60	120	48	156	78	104
160+	64	132	54	162	80	80	82	166	48	156
170+	64	108	84	172	56	120	80	116	88	178
180+	48	180	72	120	88	144	60	160	92	108
190+	72	190	64	192	96	96	84	196	60	198
200+	80	132	100	168	64	160	102	132	96	180
210+	48	210	104	140	106	168	72	180	108	144
220+	80	192	72	222	96	120	112	226	72	228
230+	88	120	112	232	72	184	116	156	96	238
240+	64	240	110	162	120	168	80	216	120	164
250+	100	250	72	220	126	128	128	256	84	216
260+	96	168	130	262	80	208	108	176	132	268
270+	72	270	128	144	136	200	88	276	138	180
280+	96	280	92	282	140	144	120	240	96	272
290+	112	192	144	292	84	232	144	180	148	264
300+	80	252	150	200	144	240	96	306	120	204
310+	120	310	96	312	156	144	156	316	104	280
320+	128	212	132	288	108	240	162	216	160	276
330+	80	330	164	216	166	264	96	336	156	224
340+	128	300	108	294	168	176	172	346	112	348
350+	120	216	160	352	116	280	176	192	178	358
360+	96	342	180	220	144	288	120	366	176	240
370+	144	312	120	372	160	200	184	336	108	378
380+	144	252	190	382	128	240	192	252	192	388
390+	96	352	168	260	196	312	120	396	198	216

Graph

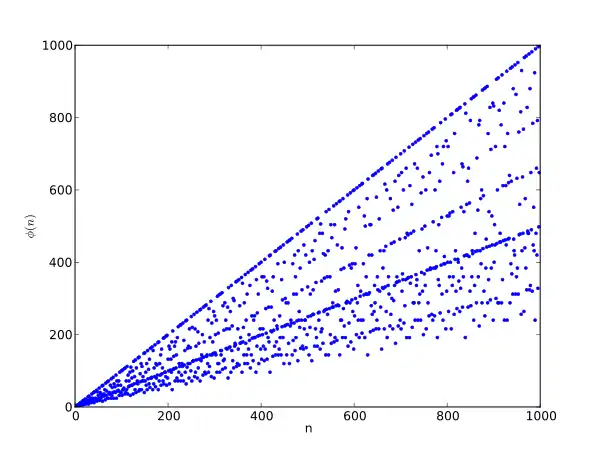${\displaystyle \varphi (n)}$ für ${\displaystyle n<1000}$