Formelsammlung Elektrotechnik: Digitaltechnik

weitere Themengebiete

Formelsammlung Elektrotechnik: Hauptseite

Rechnen mit Dualzahlen

Umrechnung Dezimalzahlen in andere Zahlensysteme

Dezimalsystem (Basis 10)	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Dualsystem (Basis 2)	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111
Oktalsystem (Basis 8)	1	2	3	4	5	6	7	10	11	12	13	14	15	16	17
Hexadezimalsystem (Basis 16)	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Umwandlung Dual - Dezimal - Hexadezimal - Oktal

Dual in Dezimal $1010=1\cdot 2^{3}+0\cdot 2^{2}+1\cdot 2^{1}+0\cdot 2^{0}=1\cdot 2^{3}+1\cdot 2^{1}=8+2=10$
Dezimal in Dual Beispiel mit Dezimalzahl 41 $\left.{\begin{matrix}41&:2&=&20&\mathrm {Rest} \ \ \mathbf {1} \\20&:2&=&10&\mathrm {Rest} \ \ \mathbf {0} \\10&:2&=&5&\mathrm {Rest} \ \ \mathbf {0} \\5&:2&=&2&\mathrm {Rest} \ \ \mathbf {1} \\2&:2&=&1&\mathrm {Rest} \ \ \mathbf {0} \\1&:2&=&0&\mathrm {Rest} \ \ \mathbf {1} \end{matrix}}\ \right\uparrow$ Ergebnis: 101001
Hexadezimal in Dezimal $4FE=4\cdot 16^{2}+15\cdot 16^{1}+14\cdot 16^{0}=1278$
Dezimal in Hexadezimal Beispiel mit Dezimalzahl 1278 $\left.{\begin{matrix}1278&:16&=&79&\mathrm {Rest} \ \ \mathbf {14} \\79&:16&=&4&\mathrm {Rest} \ \ \mathbf {15} \\4&:16&=&0&\mathrm {Rest} \ \ \mathbf {4} \\\end{matrix}}\ \right\uparrow$ Ergebnis: 4FE
Oktal in Dezimal $172=1\cdot 8^{2}+7\cdot 8^{1}+2\cdot 8^{0}=122$
Dezimal in Oktal Beispiel mit Dezimalzahl 122 $\left.{\begin{matrix}122&:8&=&15&\mathrm {Rest} \ \ \mathbf {2} \\15&:8&=&1&\mathrm {Rest} \ \ \mathbf {7} \\1&:8&=&0&\mathrm {Rest} \ \ \mathbf {1} \\\end{matrix}}\ \right\uparrow$ Ergebnis: 172

Verknüpfungsbausteine

AND-Gatter (UND-Verknüpfung)

Y=A\wedge B

Y=A\cdot B

Y=A\,B

A	B	Y
0	0	0
0	1	0
1	0	0
1	1	1

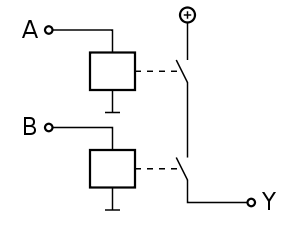weitere Bildinformationen über Formelsammlung Elektrotechnik: AND-Glied

OR-Gatter (ODER-Verknüpfung)

Y=A\vee B

Y=A+B\,

A	B	Y
0	0	0
0	1	1
1	0	1
1	1	1

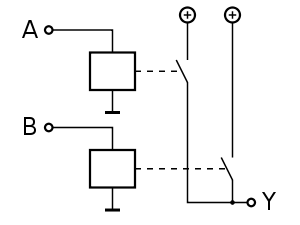weitere Bildinformationen über Formelsammlung Elektrotechnik: OR-Glied

NAND-Gatter (negierte UND-Verknüpfung)

Y={\overline {A\wedge B}}

Y=A{\overline {\wedge }}B

Y={\overline {A\,B}}

A	B	Y
0	0	1
0	1	1
1	0	1
1	1	0

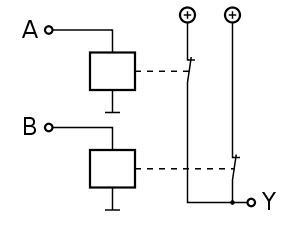weitere Bildinformationen über Formelsammlung Elektrotechnik: NAND-Glied

NOR-Gatter (negierte ODER-Verknüpfung)

Y={\overline {A\vee B}}

Y=A{\overline {\vee }}B

Y={\overline {A+B}}

A	B	Y
0	0	1
0	1	0
1	0	0
1	1	0

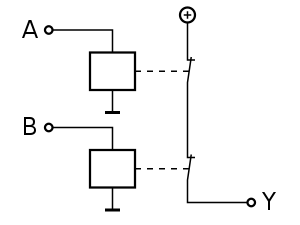weitere Bildinformationen über Formelsammlung Elektrotechnik: NOR-Glied

XOR-Gatter (Exklusiv-ODER/Antivalenz)

Y=A\,{\underline {\lor }}\,B

Y=A\oplus B

A	B	Y
0	0	0
0	1	1
1	0	1
1	1	0

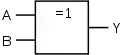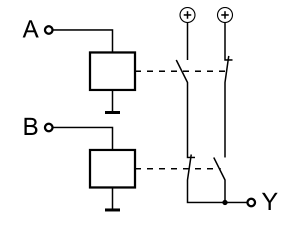weitere Bildinformationen über Formelsammlung Elektrotechnik: XOR-Glied

XNOR-Gatter (Exklusiv-NOR/Äquivalenz)

Y={\overline {A\,{\underline {\lor }}\,B}}

Y=A\,{\overline {\underline {\lor }}}\,B

Y={\overline {A\oplus B}}

A	B	Y
0	0	1
0	1	0
1	0	0
1	1	1

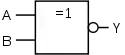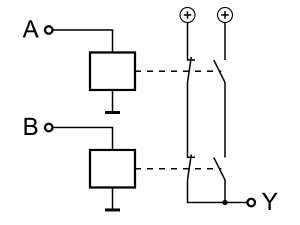weitere Bildinformationen über Formelsammlung Elektrotechnik: XNOR-Glied

Schaltalgebra - Rechenregeln für eine Variable

Kommutativgesetz (Vertauschungsgesetz)

Beispiel an einer UND-Verknüpfung:

Y=A\wedge B\wedge C=A\wedge C\wedge B=B\wedge A\wedge C=C\wedge B\wedge A

Beispiel an einer ODER-Verknüpfung:

Y=A\vee B\vee C=A\vee C\vee B=B\vee A\vee C=C\vee B\vee A

Assoziativgesetz (Verbindungsgesetz)

Beispiel an einer UND-Verknüpfung:

Y=A\wedge B\wedge C=(A\wedge B)\wedge C=(B\wedge C)\wedge A=(A\wedge C)\wedge B

Beispiel an einer ODER-Verknüpfung:

Y=A\vee B\vee C=(A\vee B)\vee C=(B\vee C)\vee A=(A\vee C)\vee B

Distributivgesetz (Verteilungsgesetz)

Beispiel in konjunktiver Form:

Y=(A\wedge B)\vee (A\wedge C)=A\wedge (B\vee C)

Beispiel in disjunktiver Form:

Y=(A\vee B)\wedge (A\vee C)=A\vee (B\wedge C)

Schaltalgebra - Rechenregeln für mehrere Variablen

De Morgansches Gesetz (Umkehrgesetz)

Umwandlung einer NAND-Verknüpfung in eine ODER-Verknüpfung

{\overline {A\wedge B}}={\overline {A}}\vee {\overline {B}}

Umwandlung einer NOR-Verknüpfung in eine UND-Verknüpfung

{\overline {A\vee B}}={\overline {A}}\wedge {\overline {B}}

Das Karnaugh-Veitch-Diagramm

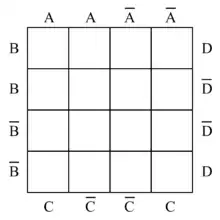Bild 1

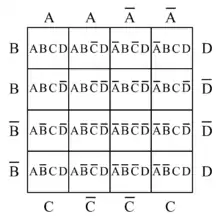Bild 2

Vereinfachung einer Funktion mit einen KV-Diagramm

Übetrage aus der Wertetabelle alle Kombinationen mit Hilfe der Disjunktive Normalform (DNF) X = 1 oder der Konjunktive Normalform (KNF) X = 0 in das KV-Diagramm

Disjunktive Normalform X = 1

A	B	C	D	X
0	1	0	0	1
0	1	0	1	1
0	1	1	1	1
1	1	0	0	1
1	1	0	1	1
1	1	1	1	1

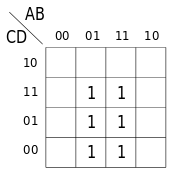Bild 3

Fasse die benachbarten Felder zu Blöcken zusammen.

Bild 4

Lese bei X = 1 die UND-Terme, bei X = 0 die ODER-Terme ab. Beim Beispiel lautet die Vereinfachung bei X = 1

$Y=(C\wedge D)\vee (C\wedge {\overline {D}})$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.