Zurück zur Übersicht

Man kann sich die Entropie als ein strömungsfähiges Etwas vorstellen, das in jedem Ding unserer Umwelt in größerer oder kleinerer Menge enthalten ist. Sie ist damit eine mengenartige Eigenschaft eines Körpers, d.h. sie bezieht sich auf einen Raumbereich und kann im weitesten Sinne wie ein „Stoff“ behandelt werden. So kann man sie in einem Materiebereich verteilen, anhäufen, einschließen oder umgekehrt daraus herauspumpen, ausquetschen, an einen anderen Gegenstand abschieben. Quelle: http://www.job-stiftung.de/pdf/skripte/Stoffdynamik/2.pdf
Anmerkungen zur Didaktik:
Zitat: Die Entropie S ist eine Größe, für die Nichtphysiker eine sehr gute Anschauung haben und mit der sie intuitiv richtig operieren. Es gibt wahrscheinlich keine andere Größe, bei der der physikalische Begriff mit einem umgangssprachlichen Begriff so gut übereinstimmt: Die meisten umgangssprachlichen Aussagen, in denen das Wort Wärme oder Wärmemenge vorkommt, bleiben physikalisch korrekt, wenn man diese Wörter durch das Wort “Entropie” ersetzt. Quelle:F. HERRMANN SKRIPTEN ZUR EXPERIMENTALPHYSIK ABTEILUNG FÜR DIDAKTIK DER PHYSIK UNIVERSITÄT KARLSRUHE AUFLAGE 2003
Das Verständnis der Entropie in der Physik und Chemie wird außerordentlich durch die Arbeiten von Herrmann, Job und dem Karlsruher Physikkurs erleichtert. Folgenden Texte sind im Internet verfügbar und als Einstieg sehr empfehlenswert:
Sehr schön erklärt wird die Entropie in der Physik in folgendem Artikel: Handreichung Entropie Uni Koblenz
Vor allem sollte man die dort angeführten Übungsaufgaben durchrechnen, dann hat man schon viel begriffen.
Sehr empfehlenswert ist auch das Ebook Georg Job, Regina Rüffler: Physikalische Chemie. Teil 1: Grundzüge der Stoffdynamik. Siehe http://www.job-stiftung.de/index.php?id=8,22,0,0,1,0
Die Wärmelehre (Thermodynamik) wird sehr gut in folgendem Buch erklärt:
Einen weiteren Versuch die Entropie in der Physik anschaulich zu erklären, hat André Thess in seinem Buch Das Entropieprinzip - Thermodynamik für Unzufriedene, Oldenbourg-Verlag 2007, ISBN 978-3-486-58428-8 mit Hilfe des Prinzips der adiabatischen Erreichbarkeit unternommen.
Entropie bei einem Phasenübergang (Schmelzen, Verdampfen, etc.)

In der Physik ist die Entropie einfach zu verstehen, wenn man den Übergang eines Stoffes in einen anderen Aggregatzustand betrachtet. Erstaunlicherweise wird dabei nur von latenter Wärme, aber selten von der Entropie gesprochen.
Man betrachtet z. B. einen Eisblock aus gefrorenem Wasser.
Will man diesen Eisblock auftauen, dann muss man am Gefrierpunkt Energie hineinstecken, ohne dass sich die Temperatur erhöht. Man spricht von der Schmelzwärme. Diese Energie dient nur dazu die bestehende Ordnung der festen Wasserteilchen aufzulösen, mehr Unordnung zu ermöglichen, das Wasser wird flüssig, die Unordnung wird größer, die Entropie wird größer.
Die Entropie beim Phasenübergang fest => flüssig entspricht der Schmelzwärme = der Schmelzenergie gemessen in Joule, da sich hier die Temperatur nicht ändert.
Diesen einfachen Umstand hat man sich auch für die Definition der Entropieeinheit zunutze gemacht:
Die Einheit der Entropie in der Physik ist 1 Joule / Kelvin.
1 Joule / Kelvin = Entropie, mit der man 0,893 cm3 Wassereis schmelzen kann. (Voraussetzung: Druck p = Normaldruck)
Man kann beim Phasenübergang die Energie also einfach durch die Temperatur des Phasenübergangs teilen und erhält die Entropiedifferenz des Vorgangs in Joule / Kelvin.
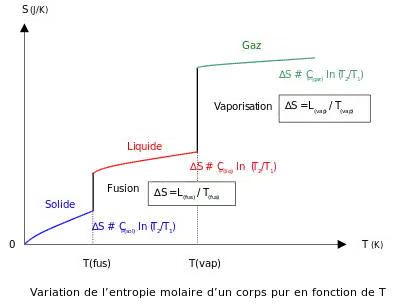
Ein sehr wichtiges Diagramm des Zusammenhanges der Entropie und der Temperatur Leider nur in Französisch.
Entropie beim Mischen eines Stoffes von zwei Teilen mit verschiedener Temperatur
Es wird eine Mischung von Wasser aus einem warmen und einem kalten Anteil betrachtet.
-------------- | | | T(w) | | warm | | | | | | ------| dE --- | V | | | | kalt | | T(k) | | | --------------
Für den kälteren bzw. wärmeren Anteil ist die Änderung der Entropien dS (Delta oder Differenz S) wie folgt definiert:
Wobei E die Wärmeenergie ist, die von dem warmen zum kalten Flüssigkeitsanteil fließt TK ist die Temperatur in Kelvin des kalten Anteils TW ist die Temperatur in Kelvin des warmen Anteils
Die gesamte Entropieänderung erhält man durch folgende Gleichung:
Dabei ist dS > 0, da TW > TK. Beachte: Die Temperaturen stehen im Nenner.
Bei diesem freiwillig ablaufenden Vorgang ist die Entropieänderung dS > 0. Erreicht die Temperatur des warmen Körpers die des kalten Körpers ist ein Gleichgewicht erreicht und der Wärmeaustausch kommt zum Erliegen.
Beispiel 1: Mischung desselben Stoffes derselben Menge unterschiedlicher Temperatur
Man füllt ein Styroporgefäß mit 300 g Wasser, das eine Temperatur von 40 Grad Celsius aufweist. Dann schüttet man 300 g Wasser von 10 Grad Celsius dazu. Das Styroporgefäß als guter Isolator nimmt nur eine minimaler Wärmemenge auf. Dann rührt man etwas herum und misst die Mischtemperatur 24,8 Grad Celsius. Als Schätzung müsste eine Mischtemperatur von 25 Grad herauskommen.
Wie kann man die Mischtemperatur errechnen?
Es gelten folgende Regeln:
- Die Energieabgabe EW der wärmeren Flüssigkeit ist gleich der Energieaufnahme EK der kälteren Flüssigkeit.
EW = EK
- Die Masse der wärmeren Flüssigkeit ist gleich der Masse der kälteren Flüssigkeit.
mW = mK
- Die spezifische Wärmekapazität des Wassers ist:
Die Temperaturen werden wie folgt bezeichnet:
- tW = 40 °C
- tK = 10 °C
- tmisch = gesucht
Es gilt folgende Formel:
EW = cWasser * m W * (tW − tmisch)
EK = cWasser * m K * (tmisch − tK)
Da EW = EK gilt, kann man vereinfachen:
cWasser * m W * (tW − tmisch) = cWasser * m K * (tmisch − tK)
Aus dieser Gleichung kürzt man cWasser. Man dividiert auf beiden Seiten durch cWasser.
m W * (tW − tmisch) = m K * (tmisch − tK)
Da im obigen Beispiel mW = mK gilt, kann man auch noch m kürzen. Es bleibt folgende Formel übrig:
(tW − tmisch) = (tmisch − tK)
Jetzt setzt man die Temperaturen ein und errechnet die Mischtemperatur:
(40 °C − tmisch) = (tmisch − 10 °C)
Jetzt rechnet man die Gleichung nach tmisch aus. Man addiert auf beiden Seiten tmisch.
40 °C − tmisch + tmisch = tmisch − 10 °C + tmisch
40 °C = 2 * tmisch − 10 °C
Man addiert auf beiden Seiten 10 °C.
50 °C = 2 * tmisch
Man dividiert beiden Seiten durch 2.
50 °C / 2 = tmisch tmisch = 25 °C
Was hat dies alles nun mit der Entropie zu tun?
Man kann aus dem obigen Beispiel jetzt auch die Entropie berechnen:
Es gilt dS = dE / TK − dE / TW
Die Temperatur muss man allerdings in Kelvin einsetzen:
TW = (40 Grad + 273 Grad) Kelvin TK = (10 Grad + 273 Grad) Kelvin
Die Energieaufnahme und -abgabe sind gleich:
EW = cWasser * m W * (tW − tmisch)
E = 4,19 J/ (g * Grad Celsius) * 300 g * (40 Grad Celsius − 25 Grad Celsius) E = 4,19 J/ (g * Grad Celsius) * 300 g * 15 Grad Celsius E = 1257 J /Grad Celsius * 15 Grad Celsius E = 18855 Joule
Daraus kann man die Entropieänderung errechnen:
dS = 18855 Joule / 283 Kelvin − 18855 Joule / 313 Kelvin dS = 66,625 − 60,24 Joule / Kelvin dS = 6,385 Joule / Kelvin
Interessant bei der ganzen Rechnung ist die Tatsache, das
- die Energie, die vom wärmeren Wasser an das kältere Wasser abgegeben wurde identisch ist mit der Energie, die das kalte Wasser aufgenommen hat.
- die Entropie des gemischten Wassers aber grösser geworden ist als die Summe der Einzelentropien vor der Mischung.
Basisgrößen der Thermodynamik und einfache Sätze
Es gibt in der Wärmelehre drei Basisgrößen:
- die Energie E
- die Temperatur T
- die Entropie S
Die Größen finden folgende Analogie in der Elektrizitätslehre:
| Thermodynamik | Elektrizitätslehre |
|---|---|
| Temperatur | elektrisches Potential |
| Temperaturdifferenz | Spannung |
| Entropie | elektrische Ladung |
| Energie | Energie |
Im Gegensatz zur elektrischen Ladung ( positiv und negative Werte) kann die Entropie nur positive Werte annehmen.
Mit diesen 3 Größen kann man einfach verstehbare Sätze über die Entropie formulieren: (Quelle Handreichung Energie und Entropie)
- Jeder Körper enthält Entropie, wenn seine Temperatur über dem absoluten Nullpunkt liegt.
- Die Entropie kann nur positive Werte annehmen.
- Je größer die Masse eines Gegenstandes ist, desto mehr Entropie enthält er, vorausgesetzt die Temperatur bleibt gleich.
- Je heißer ein Körper ist, desto mehr Entropie enthält er. Die Entropie ist also temperaturabhängig.
- Die Entropie fließt von ganz allein von einer Stelle höherer Temperatur zu einer Stelle niedriger Temperatur, wenn ein Austausch zwischen den Stellen möglich ist.
- Eine Temperaturdifferenz Delta T ist also der Anlass für einen Entropiefluss
- Je größer die Temperaturdifferenz desto größer ist der Entropiefluss unter der Voraussetzung unveränderter Materialien.
- Der Entropiefluß I ist die Entropie, welche pro Zeiteinheit geflossen ist.
VORSICHT: Nicht Groß T ( Temperatur) mit klein t (Zeit) verwechseln.
Analogie Thermodynamik und Elektrizitätslehre für abgeleitete Größen
Thermodynamik Elektrizitätslehre --------------------------------------------------------------------------------- Entropiewiderstand elektrischer Widerstand IS = Entropiefluß ΔS/Δt (t = Zeit) Ladungsfluß Ladung Q /Zeit = Stromstärke IQ Entropiekapazität CS=ΔS/ΔT elektrische Kapazität C= Ladung Q/ Spannung U IE = Energiefluß = ΔE/t = Leistung IE = Energiefluß = ΔE/t = Energie/Zeit = Leistung IE = T * IS IE = elektr.Pot * IQ ΔE = T * ΔS ΔE = elektr.Pot * ΔQ
- Jedes Material setzt dem hindurchfließenden Entropiestrom einen Widerstand entgegen.
- Dieser Widerstand ist um so größer, je kleiner die Austauschfläche A der Leitung und je größer die Länge l der Leitung ist.
- Dieser Widerstand hängt außerdem vom wärmeleitenden Material ab. Diese Materialkonstante nennt man rhoS.
- Für den Entropiewiderstand gilt also:
RS = l / A * rhoS
- Der Entropieleitwert ist der Kehrwert des Widerstandes. Er berechnet sich als
(T = Temperatur).
Dies nennt man das Fouriersche Gesetz.
- Die Entropiezunahme eines Körpers bei Erhöhung der Temperatur nennt man Entropiekapazität CS. Sie berechnet sich als
- Die Entropiekapazität hängt vor allem von der Temperatur, aber auch von der Masse, dem Volumen, dem Druck und der Stoffmenge ab.
- Bei Phasenübergängen wie dem Schmelzen und Verdampfen ändert sich die Entropiekapazität sehr stark.
- Entropie kann neu erzeugt werden durch
- Reibung
- eine chemische Reaktion
- durch elektrische Ströme in elektrischen Widerständen
- durch Entropieströme in Wärmewiderständen.
- Entropie kann zwar erzeugt, aber in der Summe nicht verringert werden.
- Vorgänge, bei denen Entropie erzeugt wird, können von alleine nicht wieder rückwärts ablaufen. Sie sind irreversibel.
- Die Entropie ist ein Energieträger. Liegt ein Entropiefluss vor, so ist dieser immer von einem Energiefluss begleitet.
- Die den Entropiefluss IS begleitende Energiefluß (Energiestromstärke) IE berechnet sich zu
Lässt man den Faktor Zeit aus der Formel auf beiden Seiten wegfallen, dann ergibt das:
- Die Energiestromstärke entspricht einer Leistung (Energie / Zeit).
P = IE
- Versucht man mit verschiedenen Arten des Wärmeentzugs einem Körper immer mehr Energie zu entziehen, kann man zwei Tatsachen feststellen:
- Man kommt zwar der Temperatur Null Kelvin (-273.15 Grad Celsius) sehr nahe, kann sie aber nicht unterschreiten bzw. erreichen. Bei dieser Temperatur befindet sich ein absoluter Temperaturnullpunkt.
- Bei dieser Temperatur kann man keine Entropie mehr entziehen. Absolut kalte Körper haben keine Entropie mehr.
- Die Einheit der Entropie in der Physik ist 1 Joule / Kelvin.
- 1 Joule / Kelvin entspricht der Entropiemenge, mit der man bei Normaldruck 0,893 cm3 Wassereis schmelzen kann.
- Manche Autoren verwenden das Carnot (Einheitenzeichen: Ct) aus didaktischen Gründen als besonderen Namen für die SI-Einheit Joule durch Kelvin (J/K) der Entropie.
Messung der Entropie
Entgegen einer weit verbreiteten Meinung ist die Entropie in der Physik relativ einfach zu messen.
Ein einfaches Beispiel zeigt die Messung der Schmelzwärme oder der Verdampfungswärme verschiedener Stoffe. Da hier die Temperatur konstant ist, kann man die ermittelte Energie direkt der Entropie gleichsetzen.
Peltierelement
Entropieströme durch eine Fläche lassen sich mit einem geeichten Peltier-Element messen.
Rechenaufgaben

Aufgabe 0
Sie haben 1 Liter Wasser von 20 Grad. Dazu gießen Sie einen weiteren Liter Wasser von 20 Grad dazu. Frage a: Wie hoch ist danach die Temperatur des Wassers ? Frage b: Wie groß ist danach die Entropie`?
Antwort: Die Temperatur bleibt gleich. Die Entropie verdoppelt sich.
Aufgabe 1
1. Sie haben 1 kg Eis bei Null Grad Celsius und normalem Umgebungsdruck. Berechnen Sie die Zunahme der Entropie, wenn das Eis komplett zu Wasser von 0 Grad geschmolzen ist. Benutzen Sie dazu die spezifische Schmelzwärme von Wasser.
- Lösung: S = 1219,848 Joule / Kelvin
- Lösungsweg: Siehe Entropie: Loesungen
1a. Sie haben 5 kg Wasser beim normalen Siedepunkt von 100 Grad Celsius und normalem Umgebungsdruck. Berechnen Sie die Zunahme der Entropie, wenn das Wasser komplett zu Wasserdampf mit der Temperatur des Siedepunktes verdampft ist. Benutzen Sie dazu die spezifische Verdampfungswärme (Verdampfungsenthalpie) von Wasser. (Siehe de.wikipedia.org/wiki/Verdampfungswärme#Verdampfungsenthalpie)
- Lösung: S =
- Lösungsweg: Siehe Entropie: Loesungen
1b. Warum muss bei dem Vorgang Energie aufgewendet werden und warum läuft die Verdampfung nicht von alleine ab? Wann läuft die Verdampfung scheinbar von alleine ab?
1c. Kommt es bei dem Übergang Wasser > Wasserdampf zu einer Entropiezunahme oder Entropieabnahme?
1d. Wie kann man sich erklären, das Wasser auch bei normalen Luftdruck auch schon bei Temperaturen weit unter dem Siedepunkt verdampft z. B. bei der Trocknung eines Wäschestückes auf der Wäscheleine?
Aufgabe 2
2. Sie erwärmen 1 kg Wasser von 20 Grad Celsius auf 70 Grad Celsius. Wieviel Energie müssen Sie dazu verwenden? Wie groß ist die Entropiezunahme?
- Lösung: S =
- Lösungsweg: Siehe Entropie: Loesungen
Aufgabe 3
3. Sie mischen 1 kg Wasser von 20 Grad Celsius und 1 kg Wasser von 50 Grad Celsius. Wieviel Energie geht vom wärmeren Wasser auf das kältere Wasser über? Wie hoch ist die Mischtemperatur? Wie groß ist der Entropieanstieg?
- Lösung: S =
- Lösungsweg: Siehe Entropie: Loesungen
Aufgabe 4
10 kg Stickstoff werden isobar auf 1/10 des Anfangsvolumens verdichtet .
- Wie ändert sich der Druck ?
- Wie ändert sich die Temperatur ?
- Wie ändert sich die Entropie ?
- Wieviel mechanische Energie muß dafür aufgewendet werden ?
Aufgabe 5
Die spezifische Wärmekapazität des Wassers Cw ist bei p = 1 atm gleich 4,19 J / (g*K). Erklären Sie diesen Wert für 1 g Wasser und 1 Grad Kelvin Temperaturerhöhung.
Aufgabe 6
Welche Wassermenge hat bei 50 Grad die gleiche Wärmemenge (Entropie ) wie 2000 g Wasser bei 20 Grad Celsius ?
Aufgabe 7
Der Heizdraht eines 1200-W-Haarföns hat eine Temperatur von 1000 K.
- Wie viel Entropie wird pro Sekunde im Heizdraht erzeugt?
Aufgabe 8
Berechnen sie die Entropie die notwendig ist, um 5 kg Eis bei Null Grad Celsius und p = 1 atm zum Schmelzen zu bringen.
Wie kann man das berechnete Ergebnis mit einem Tauchsieder meßtechnisch überprüfen ?
Wie unterscheidet sich der Wert der Entropie, die dafür notwendig ist, vom errechneten Wert der Energie ?
Aufgabe 9
Berechnen sie die Entropie die notwendig ist, um 5 kg Wasser von Null Grad Celsius und p = 1 atm auf 10 Grad Celsius und gleichbleibendem Druck zu erwärmen ?
Wie kann man das berechnete Ergebnis mit einem Tauchsieder meßtechnisch überprüfen ?
Aufgabe 10
Wie ändert sich die Entropie S in einem Stück Metall mit der Masse m = 0,001 kg beim Anstieg der Temperatur von 1 Grad Kelvin auf 11 Grad Kelvin ?
Nehmen Sie dazu an, daß die spezifische Wärmekapazität c des Metalls konstant 500 J/kg/Kelvin beträgt.
Benutzen Sie folgende Formel:
T2 ist die Temperatur 11 Kelvin T1 ist die Temperatur 1 Kelvin ln = Logarithmus zur Basis e (natürlicher Logarithmus)
Lösung:
Delta S = 500 J/kg/Kelvin * 0,001 kg * ln ( 11 / 1 ) Delta S = 0,5 J/K * 2,397 Delta S = 1,2 J/K
Aufgabe 11 Mischung von Gasen
Ein 10-Liter Behälter ist in zwei gleiche Hälften geteilt. In einer befindet sich Stickstoff mit einem Druck von 1 bar, in der anderen Hälfte Wasserstoff von 1 bar. Die Temperatur ist 20 Grad Celsius.
- Wie ändert sich die Entropie S und die freie Enthalpie G des Gesamtsystems, wenn man eine Vermischung zulässt ?
- Wie lange dauert es , bis eine gleichmässige Vermischung der beiden Gase erreicht ist ?
- Wie groß ist ΔS und ΔG, wenn der Wasserstoff durch Stickstoff ersetzt wird ?
Aufgabe 12 Mischung von 2 idealen Gasen
Wir mischen zwei Gase adiabatisch mit gleichen Volumina, gleicher Temperatur, gleicher Teilchenzahl . Beispielsweise 1 Mol Helium und 1 Mol Neon.
Berechnen Sie mit der Boltzmann Konstante k und der Avogadroschen Zahl die Mischungsentropie.
Daraus ergibt sich:
- DeltaS = k * NA * ln (( NA + NA ) / NA ) + k * NA * ln (( NA + NA ) / NA)
- DeltaS = 2*k *NA * ln 2
- DeltaS = 2* 1,380*10^-23 J/K* 6,02214179*10^23 1/mol*ln2
- DeltaS = 2*1,4*6,02*0,69 J/K/mol
- DeltaS = 11,68 J/K/mol
Aufgabe 13
Sie betrachten ein Gas mit folgenden Vorgaben:
- Temperatur 290 K
- Volumen 1 m3
- Druck 1,5 bar
Berechnen Sie die Gesamtentropie des Gases.
- Welche Formel wollen Sie benutzen ?
- Woe lautet das Ergebnis ?
- Welche Einheit hat das Ergebnis ?
- Wie kann man das Ergebnis interpretieren ?
Zweiter Hauptsatz der Thermodynamik
Jeder Körper enthält Entropie.
Entropie kann nur zusammen mit Wärme von einem Körper zu einem anderen Körper übertragen werden.
Dabei gilt: Übertragene Wärme / übertragene Entropie = Temperatur
Entropie kann produziert aber niemals vernichtet werden.
In einem abgeschlossenen System kann die Gesamtentropie nicht abnehmen. Sie bleibt im Laufe der zeitlichen Entwicklung dieses Systems entweder konstant oder sie nimmt zu.
Für abgeschlossene Systeme gilt:
Verweise
- www.wiwi.uni-frankfurt.de/~rainerh/Diplomarbeit/dbdzh03.htm
- 2. Hauptsatz gut lesbar erklärt
- de.wikipedia.org/wiki/Thermodynamik
- Thermodynamik
Nullpunktentropie
Aus theoretischen Erwägungen heraus müssten Kristalle am absoluten Nullpunkt eigentlich die Entropie 0 haben. Das ist jedoch selten der Fall. Meist schaffen es reale Kristalle, nach dem sie einmal erstarrt sind, nicht mehr, die ideal mögliche Kristallordnung mit 0 Entropie anzunehmen. Die messbare reale, von 0 verschiedene Entropie der Kristalle am absoluten Nullpunkt der Temperatur wird Nullpunktentropie genannt.
Thermodynamisches Gleichgewicht
Jedes abgeschlossene thermodynamische System, in dem gewisse Austauschprozesse frei möglich sind, nimmt nach dem Abklingen der Prozesse einen Gleichgewichtszustand an. Dieser ist bestimmt durch das Maximum der Entropie dieses Systems.
siehe auch Definition der Entropie über das Prinzip der adiabatischen Erreichbarkeit.
Lokale Entropieabnahme
Es gibt viele Beispiele für eine lokale Entropieabnahme, die vermeintlich dem 2. Hauptsatz widersprechen, die aber durch eine Gesamtbetrachtung schlüssig erklärt werden können. Es entstehen geordnete Strukturen aus vorher ungeordneten. Gleichzeitig wird aber dafür die Entropie insgesamt trotzdem größer
Beispiele
- Sternentstehung durch Gravitation
- Kristallisation von Stoffen beim Abkühlen
- Lebensentstehung auf der Erde
- Evolution des Lebens auf der Erde.
Auch die Vorstellung vom Urknall geht von einem sehr entropiearmen Anfangszustand aus. Irgendwie muss dieser entropiearme Zustand erreicht worden sein.
Entropieformel von Boltzmann
Zitat aus dem Spiegel Wissenslexikon http://www.spiegel.de/lexikon/54415448.html
L. Boltzmann erkannte, dass der Entropiesatz gleichbedeutend ist mit folgender Wahrscheinlichkeitsaussage: Die auf die einzelnen Moleküle eines Körpers verteilte Bewegungsenergie geht stets von einem weniger wahrscheinlichen Verteilungszustand in einen wahrscheinlicheren über, nicht aber umgekehrt. Sind z. B. alle Luftmoleküle zu Anfang in einer Ecke eines Zimmers, so verteilen sie sich gleichmäßig in diesem Zimmer: die Entropie nimmt zu. Es ist jedoch praktisch ausgeschlossen, dass umgekehrt die gleichmäßig verteilten Moleküle sich einmal alle in einer Zimmerecke ansammeln.