Bewegungsgleichung einer freien Teilchens mit der Lagrange Gleichung

Ein Pendel bewege sich im festen Abstand ${\displaystyle l}$ in der der x,y,z-Ebene.

Skizze eines sphärischen Pendels

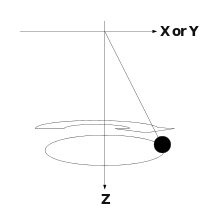
Berechne die Bewegungsgleichung eines sphärischen Pendels, mithilfe der Lagrangen-Bewegungsgleichung.

Aufstellen der Lagrangen-Bewegungsgleichungen

Das System hat eine Zwangsbedingung:

${\displaystyle |{\vec {r}}|-l=0}$

Wir finden daher ${\displaystyle 3-1=2}$ generalisierte Koordinaten.

Da sich das Teilchen auf einer Kugeloberfläche mit dem festen Abstand ${\displaystyle l}$ vom Nullpunkt.

Daher wählt man als generalisierte Koordinaten die beiden Winkel ${\displaystyle \varphi }$ und ${\displaystyle \vartheta }$, und schreibt ${\displaystyle {\vec {r}}}$ in Kugelkoordinaten:

${\displaystyle {\vec {r}}=\left(\!{\begin{array}{c}|{\vec {r}}|\sin(\vartheta )\cos(\varphi )\\|{\vec {r}}|\sin(\vartheta )\sin(\varphi )\\|{\vec {r}}|\cos(\vartheta )\end{array}}\!\right){\overset {\text{vgl. Zwangsbedingung}}{=}}l\cdot {\hat {e}}_{r}(\vartheta ,\varphi )}$

Nun stellt man die kinetische Energie als Funktion von ${\displaystyle \vartheta }$, ${\displaystyle {\dot {\vartheta }}}$ , ${\displaystyle \varphi }$ und ${\displaystyle {\dot {\varphi }}}$ dar.

${\displaystyle T({\dot {\vartheta }},\vartheta ,{\dot {\varphi }},\varphi )={\frac {1}{2}}m{\vec {v}}^{2}={\frac {1}{2}}m\left(l\cdot {\frac {d}{dt}}{\hat {e}}_{r}\right)^{2}=}$

Nebenrechnungen

Berechne ${\displaystyle {\frac {d}{dt}}{\hat {e}}_{r}={\frac {\partial {\hat {e}}_{r}}{\partial \varphi }}\cdot {\dot {\varphi }}+{\frac {\partial {\hat {e}}_{r}}{\partial \vartheta }}\cdot {\dot {\vartheta }}+\underbrace {\frac {\partial {\hat {e}}_{r}}{\partial t}} _{=0}}$ ${\displaystyle ={\dot {\varphi }}\underbrace {\left(\!{\begin{array}{c}-\sin(\vartheta )\sin(\varphi )\\\sin(\vartheta )\cos(\varphi )\\0\end{array}}\!\right)} _{=e_{\varphi }}+{\dot {\vartheta }}\underbrace {\left(\!{\begin{array}{c}\cos(\vartheta )\cos(\varphi )\\\cos(\vartheta )\sin(\varphi )\\-\sin(\vartheta )\end{array}}\!\right)} _{=e_{\vartheta }}}$ ${\displaystyle ={\hat {e}}_{\varphi }\cdot {\dot {\varphi }}+{\hat {e}}_{\vartheta }\cdot {\dot {\vartheta }}}$ sphärisches Pendel mit dem Winkel ${\displaystyle \vartheta }$

${\displaystyle ={\frac {1}{2}}m\cdot l^{2}\left({\hat {e}}_{\varphi }\cdot {\dot {\varphi }}+{\hat {e}}_{\vartheta }\cdot {\dot {\vartheta }}\right)^{2}}$

${\displaystyle ={\frac {1}{2}}m\cdot l^{2}\left({\dot {\varphi }}^{2}(\sin ^{2}(\vartheta )\underbrace {(\sin ^{2}(\varphi )+\cos ^{2}(\varphi ))} _{=1})+{\dot {\vartheta }}^{2}\underbrace {(\sin ^{2}(\vartheta )\underbrace {(\sin ^{2}(\varphi )+\cos ^{2}(\varphi ))} _{=1}+\cos ^{2}(\vartheta )} _{=1})+2\underbrace {\cdot {\hat {e}}_{\varphi }{\dot {\varphi }}\cdot {\hat {e}}_{\vartheta }{\dot {\vartheta }}} _{=0,\ da\ {\hat {e}}_{\varphi }\perp {\hat {e}}_{\vartheta }}\right)}$

${\displaystyle ={\frac {1}{2}}m\cdot l^{2}\left({\dot {\varphi }}^{2}\sin ^{2}(\vartheta )+{\dot {\vartheta }}^{2}\right)=T({\dot {\varphi }},{\dot {\vartheta }},\vartheta )}$

Die potentielle Energie wird wie folgt in generalisierten Koordinaten ausgedrückt:

${\displaystyle V({\vec {r}})=-mg\cdot {\vec {r}}_{z}=-mg\cdot l\cdot \cos(\vartheta )=V(\vartheta )}$

Die Lagrange Funktion lautet also:

${\displaystyle L={\frac {1}{2}}m\cdot l^{2}\left({\dot {\varphi }}^{2}\sin ^{2}(\vartheta )+{\dot {\vartheta }}^{2}\right)+mg\cdot l\cdot \cos(\vartheta )}$

Berechnen der generalisierten Bewegungsgleichnungen

Berechnet man nun also die Lagrangefunktion, so ergeben sich daraus die generalisierten Bewegungsgleichungen:

${\displaystyle 0={\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\varphi }}}}-{\frac {\partial L}{\partial \varphi }}={\frac {d}{dt}}m\cdot l^{2}\sin ^{2}(\vartheta ){\dot {\varphi }}}$

${\displaystyle \Longrightarrow m\cdot l^{2}\sin ^{2}(\vartheta ){\dot {\varphi }}=const.}$ (1) - z-Komponente des Drehimpulses ${\displaystyle =m\left({\vec {r}}\times {\vec {v}}\right)_{z}}$, die Winkelgeschwindigkeit ${\displaystyle \vartheta }$ bleibt konstant. Wird ${\displaystyle \vartheta }$ kleiner, so muss ${\displaystyle \varphi }$ größer werden, um den Term konstant zu halten. Da der Ausdruck konstant ist, kann das Pendel, in diesem reibungsfreien Fall niemals den z-Nullpunkt durchlaufen - der Drehimpuls bleibt also erhalten.

${\displaystyle 0={\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\vartheta }}}}-{\frac {\partial L}{\partial \vartheta }}=ml^{2}{\ddot {\vartheta }}-(ml^{2}{\dot {\varphi }}^{2}\sin(\vartheta )\cos(\vartheta )-mgl\cdot \sin(\vartheta ))}$

Wir formen die z-Komponente des Drehimpulses nach ${\displaystyle {\dot {\varphi }}}$ so um, das man sie in die ${\displaystyle \vartheta }$-Bewegungsgleichung einsetzen kann, sodass diese keine ${\displaystyle {\dot {\varphi }}}$-Abhängigkeit mehr hat.

${\displaystyle {\frac {c}{m\cdot l^{2}\sin ^{2}(\vartheta )}}={\dot {\varphi }}}$

${\displaystyle ml^{2}{\ddot {\vartheta }}=ml^{2}\sin(\vartheta )\cos(\vartheta )\cdot {\frac {c^{2}}{m^{2}\cdot l^{4}\sin ^{4}(\vartheta )}}-mgl\cdot \sin(\vartheta )}$

${\displaystyle \Rightarrow {\ddot {\vartheta }}=\sin(\vartheta )\cos(\vartheta )\cdot {\frac {c^{2}}{m^{2}\cdot l^{4}\sin ^{4}(\vartheta )}}-{\frac {g}{l}}\cdot \sin(\vartheta )}$

Diese Differentialgleichung 2ter Ordnung könnte nun z. B. numerisch per Computer gelöst werden.

Bestimmt man so ${\displaystyle \vartheta (t)}$, so kann damit durch einsetzen in Gleichung (1) auch ${\displaystyle {\dot {\varphi }}(t)}$ bestimmt werden, sodass so der genaue Ortsvektor des Teilchens zu jedem Zeitpunkt ${\displaystyle t}$ bestimmt werden kann.