.svg.png.webp)
Finde mittels der Variation der Kurve, nach den Prinzipien der Variationsrechnung den kürzesten Weg S zwischen den Punkten A und B auf einer homogenen Ebene.
1. Finde die Funktionenschar
Formuliere den allgemeinen Integranden in eine für das Problem geeignete Form um. Wie würdest Du die Teilstrecke mathemathisch formulieren?
Lösungshinweis 1
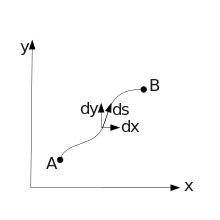
Lösung der Aufgabe 1
kann in karthesischen Koordinaten nach dem Satz des Pythagoras wie folgt dargestellt werden:
2. Aufstellen der Eulerschen Gleichung
Stelle nun zunächst das Integral für den Weg auf.
Stelle dann die Eulersche Gleichung auf und löse diese.
Lösung der Aufgabe 2
- Die Eulersche Gleichung lautet:
- Dabei ist:
- Damit folgt und somit
- Sei . Es folgt
- Wegen ist für bestimmte und damit ist eine Gerade.
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.